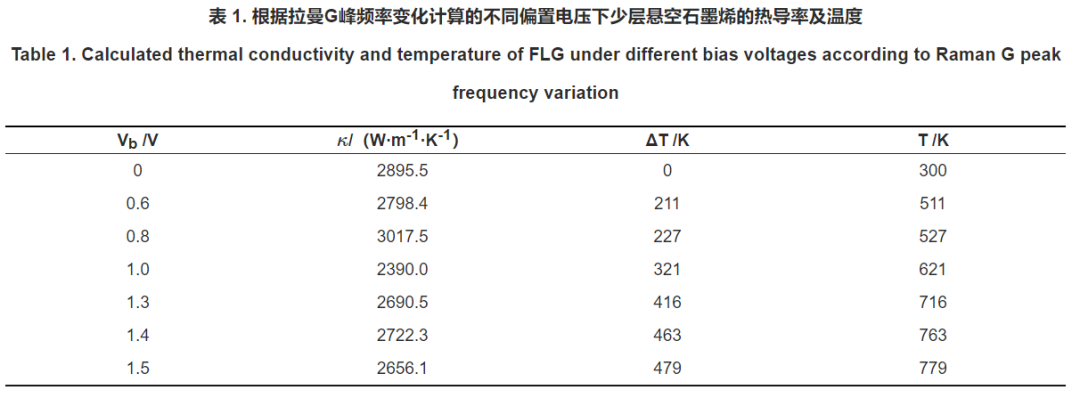
石墨烯是典型的二维原子晶体材料，具有极高的热导率，其以独特的电子-声子相互作用机制以及在微纳尺度热管理领域的应用潜力而备受瞩目。国内外针对石墨烯在不同温度下的热导率进行了大量的理论和实验研究，但如何准确测量电偏置作用下悬空石墨烯器件的热导率仍需进一步深入研究。本课题组成功制备了高质量的悬空石墨烯场效应晶体管，并基于拉曼光谱法研究了少层悬空石墨烯在不同电压下的热导率变化规律。实验结果显示：当偏置电压从0 V增加至1.5 V时，悬空石墨烯的最大温度变化范围为300~779 K，同时其热导率也发生了相应变化，介于2390~3000 W/（m·K）之间。本实验结果为研究悬空石墨烯纳米电子器件在实际应用场景中的热传导特性提供了实验数据参考。

　　随着半导体制备技术的快速发展以及新型二维材料的涌现，半导体器件的尺寸不断缩小至微纳尺度，器件的集成化越来越高，但器件的产热也集中在更小的范围内，热能密度成倍增大，散热问题成为制约微纳器件尺寸进一步缩小的主要问题。因此，微纳器件的热管理不容忽视。热导率作为材料的关键热特性参数之一，对于优化微纳器件的热管理至关重要。热导率的确定通常需要测量样品的温度或热流量，并结合公式或数值模型来完成。例如，块体材料的热导率一般采用3ω法进行测量，而纳米材料的热导率通常采用拉曼光谱法、悬空热桥法以及时域热反射法测量［1-6］。在众多的新材料中，石墨烯、硼烯［7］、二硫化钼［8-9］、二硫化钨［10］等二维层状材料具有原子级厚度以及优异的热导率，很适合用于微纳尺度器件的热管理。其中，石墨烯是由碳原子以sp2杂化形成的以蜂窝状晶格排列而成的单原子层材料，厚度仅为0.34 nm，是目前已知最薄的材料，具有优异的电学、光学和热学性能［11-15］。2008年，加州大学河滨分校的Balandin课题组［1］利用拉曼光谱法对单层石墨烯的热导率进行了测量，结果显示其热导率最高可达5300 W/（m·K），高于块体石墨与金刚石的热导率，是目前所知材料中最高的，引起了研究人员的广泛关注。石墨烯是一种良好的二维导热填料，在热界面材料中具有广阔的应用前景。在此应用背景下，诸多学者研究了衬底、褶皱、应变及晶粒尺寸对石墨烯热导率的影响。2010年，得克萨斯大学的Ruoff课题组［6］测量了通过化学气相沉积（CVD）在铜衬底上生长的单层石墨烯在悬空与支撑状态下的热导率，结果表明，铜衬底与二氧化硅衬底上的单层石墨烯的热导率相近。2011年，新加坡国立大学的Thong课题组［16］采用悬空热桥法对悬空和衬底支撑的少层石墨烯在77~350 K温度范围内的热导率进行了测量，验证了衬底的存在会降低石墨烯的热导率。2012年，厦门大学的蔡伟伟课题组［17］研究了CVD生长的悬空石墨烯的褶皱对热导率的影响，他们对无褶皱和有褶皱石墨烯的热导率进行统计后发现，无褶皱石墨烯热导率的平均值比有褶皱石墨烯的高27%。2017年，中国科学院金属研究所的任文才课题组［18］通过一种分离-吸附化学气相沉积方法实现了铂（Pt）衬底上晶粒大小可控的单层石墨烯的生长，并研究了晶粒尺寸在200 nm~1 μm范围内的单层石墨烯热导率的变化规律，结果发现石墨烯薄膜的热导率随着晶粒尺寸的减小而显著降低。2022年，大阪府立大学的Arie课题组［19］研究了石墨烯在施加双轴拉伸应变时热导率的变化，他们在实验中采用拉曼光谱仪和原子力显微镜精确估计应变；结果表明：当应变为0.1%时，石墨烯的热导率急剧降低了约70%。总结前人关于悬空石墨烯热导率的研究发现，石墨烯中温度的变化多数来源于环境温度的变化（环境温度变化是由于将基底作为加热源，或者通过照射拉曼激光引入了热量）。鉴于此，本课题组结合拉曼光谱法，针对电偏置作用下的少层悬空石墨烯的热导率展开研究。石墨烯中的温度变化过程是一个连续变化的动态过程，是由外加偏置电压主导的，而非简单的环境温度变化。在这个过程中，热电子通过电子-声子耦合机制将热量传递给石墨烯晶格。以单层石墨烯为例，其总共有6支声子色散曲线个光学支（面内纵向光学支iLO、面内横向光学支iTO和面外横向光学支oTO）和三个声学支（面内纵向声学支iLA、面内横向声学支iTA和面外横向声学支oTA），其中涉及石墨烯中的热电子与这些声子之间较为复杂的耦合机制与平衡状态。本课题组首先通过对不同温度下的少层悬空石墨烯（简称为“FLG”）进行变温拉曼光谱测试，计算出石墨烯拉曼特征峰的一阶温度系数，然后基于拉曼光谱法研究不同偏置电压作用下少层悬空石墨烯的温度及热导率变化。

　　悬空石墨烯器件的制作分为三步：1）制作电极；2）刻蚀沟道；3）转移石墨烯。第一步包括以下几个步骤：1）在硅片表面旋涂AZ5214光刻胶，并在100 ℃下烘烤1 min，减小光刻胶的流动性，使之定型；2）使用紫外光刻进行曝光，显影定影后，得到所需的电极图案；3）采用电子束热蒸镀工艺先后在曝光区域蒸镀厚度分别为5 nm的铬（Cr）层和50 nm的金（Au）层，通过剥离（lift-off）工艺得到所需的金属电极。第二步使用电感耦合等离子体刻蚀机（ICP）对电极之间的SiO2层进行刻蚀，得到刻蚀沟道，沟道宽度为1.0 μm，深度为300 nm。第三步所用的石墨烯是由高定向热解石墨薄片通过机械剥离得到的，石墨烯的转移采用的是基于聚二甲基硅氧烷和聚乙烯醇树脂薄膜（PDMS+PVA）的干法转移，即：加热转移载体，PDMS反复释放PVA，从而实现石墨烯从硅片到电极上方的转移，得到所需器件。

　　在热导率测量实验中，通过改变电极两端的偏置电压，在电流焦耳热作用下改变石墨烯的温度。固定偏置电压，改变拉曼光谱仪的激光功率，测量石墨烯的拉曼光谱，如图1（a）所示。图1（b）为悬空石墨烯器件的扫描电子显微镜图像，图1（c）为后续加电测试的石墨烯拉曼单点光谱与器件的扫描电子显微镜照片。根据拉曼光谱可以判断石墨烯的层数为4~5层；扫描电子显微镜照片清晰地表明石墨烯悬空状态良好，没有塌陷与破损。值得注意的是，通过PDMS+PVA干法转移的石墨烯器件通常会存在不可避免的聚合物残留。使用探针台与2636B源表对器件进行电流退火，可以减少石墨烯上残留的PVA，减少掺杂，显著提高器件的迁移率，同时保证后续测试过程的稳定性。图1（d）是石墨烯器件经电流退火后在室温下测得的场效应转移曲线I–Vg，石墨烯器件的电中性点VD=3.47V，这表明石墨烯掺杂很少。

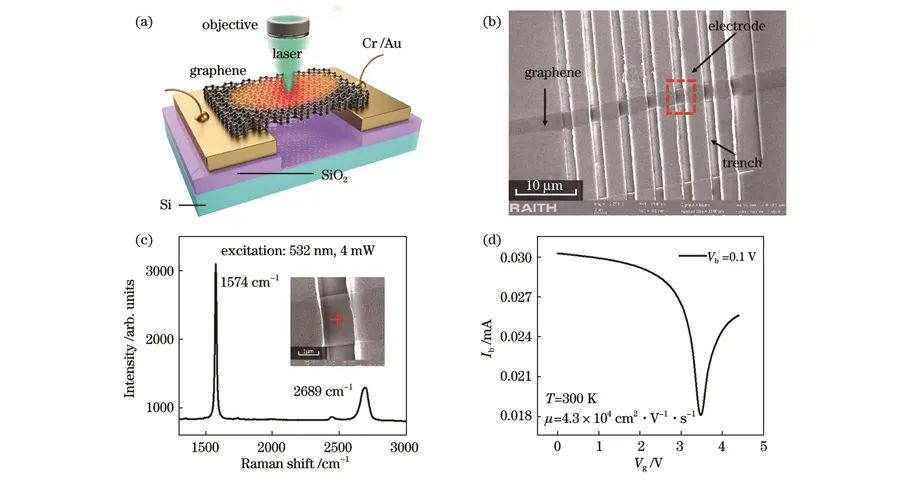
　　图 1. 悬空石墨烯器件示意图及表征测试。（a）器件结构以及拉曼光谱仪测量热导率的实验示意图；（b）悬空石墨烯器件的扫描电子显微镜（SEM）照片；（c）少层悬空石墨烯的拉曼光谱；（d）少层悬空石墨烯晶体管的场效应转移曲线

　　材料的拉曼特性对外部环境变化具有很高的敏感性，如应力、温度等外部因素发生改变时，拉曼光谱的特征峰频率会发生相应变化［20-24］。采用拉曼光谱法测定二维材料的热导率通常分为两步：

　　1） 标定石墨烯的温度系数。通过改变环境温度，获得不同温度下石墨烯的拉曼光谱，确定温度与特征峰频率的关系，得到一阶温度系数χ。

　　2） 固定偏置电压，改变激光功率，获得不同激光功率下石墨烯的拉曼光谱，确定激光功率与特征峰频率的关系，计算得到热导率κ。

　　对于单层悬空石墨烯的热输运过程，可以考虑两种极端情况［1］，一种是热量从石墨烯的中心向边界扩散，另一种是热量以平面波的形式以相反的方向向两侧沟道传播。前者适用于激光光斑远小于悬浮石墨烯尺寸的情况，后者则适用于激光光斑大小与石墨烯宽度W相当的情况。基于两个不同激光功率（P1和P2）下的器件中心点温度，可以建立均匀径向热流方程，得到关于热导率的表达式κ=χ(1/2πh)(ΔP/ΔT)−1，其中h是单层石墨烯的厚度，ΔT是两个激光功率下单层石墨烯的温度变化。

　　式中：L、h、W分别为刻蚀沟道上方少层悬空石墨烯的长度、厚度与宽度；δω为激光加热功率δP导致的特征峰峰值频率的位移；χ为石墨烯拉曼特征峰的一阶温度系数，需要单独进行计算；ω0为计算所得0 K下的拉曼特征峰频率。在一定温度范围内，当温度发生变化时，石墨烯的晶格结构也会随之发生变化，导致拉曼特征峰发生变化，即：温度升高时，拉曼特征峰红移；温度下降时，拉曼特征峰蓝移。拉曼峰值处的频率随着样品温度变化近似呈线）所示。此前使用拉曼光谱法测量石墨烯温度的研究也因此将石墨烯的G峰与2D峰作为温度计。该式也可以写成Δω=χΔT，其中Δω是由温度变化引起的拉曼特征峰频率的变化，ΔT为温度变化，即通过变温拉曼光谱下石墨烯特征峰的频率变化可以计算得到材料拉曼特征峰的一阶温度系数。

　　石墨烯吸收激光后温度升高，导致其晶格结构发生改变，因此，激光光斑处的石墨烯的温度可由G峰或2D峰的频率偏移来估算。过去的大部分研究是针对硅基底上的石墨烯体系进行的，除了热效应以外，拉曼光谱还会受到应变（由基底与石墨烯热膨胀系数不同引起）的影响

　　。研究表明，悬空石墨烯的中心远离电极，热能耗散率低，热量容易累积。本课题组在进行拉曼光谱测试时，均将激光对准悬空石墨烯中心，激光波长为532 nm。

　　图 2. 石墨烯变温拉曼光谱以及G峰、2D峰的频率变化。（a）100~400 K范围内少层悬空石墨烯的变温拉曼光谱；（b）不同温度下的石墨烯G峰频率以及计算得到的一阶温度系数χGχG；（c）不同温度下的石墨烯2D峰频率以及计算得到的一阶温度系数χ2D

　　图2（a）为不同温度下测得的石墨烯的拉曼光谱，G峰、2D峰的峰位变化由黑色虚线标出，可以看出：当温度升高时，石墨烯的G峰频率减小，发生红移；当温度降低时，G峰频率增大，发生蓝移。2D峰也出现相同的趋势，同时在温度升高时会发生展宽。图2（b）、（c）分别是从石墨烯变温拉曼光谱中提取的G峰与2D峰的频率，频率与温度之间的变化关系可以用Δω=χΔT描述。拟合后的结果表明，石墨烯G峰的一阶温度系数χ

　　可知，石墨烯的G峰与2D峰都可以用来判断石墨烯的局部温度变化。对于单层石墨烯而言，2D峰表现出明显的对称性，其频率可由单个洛伦兹峰拟合得到；随着石墨烯层数增加，2D峰的对称性逐渐消失，频率须由多个洛伦兹峰拟合得到。对于少层悬空石墨烯来说，继续采用2D峰进行拟合将不再合适，因此本文用G峰进行拟合，同时采用对应的一阶温度系数χ

　　接下来采用光功率计确定少层悬空石墨烯上的拉曼激光功率。由图3（a）可以明显看出，当偏置电压为零时，随着激光功率由0.5 mW增大到4.0 mW，少层悬空石墨烯的G峰发生红移，频率减小，峰强明显增大。这表明少层悬空石墨烯中心位置的局部温度升高。图3（b）展示了少层悬空石墨烯的G峰频率与激光功率之间的关系，通过线性拟合得到斜率δωδP=−0.5698。该样品的长度L=1.0 μm，宽度W=2.8 μm，厚度h=1.7 n。